資料結構 HW2 Paper work
目錄
作者
4112064214 | 侯竣奇 | 電資學士班
答案僅供參考,如有錯誤歡迎指正。
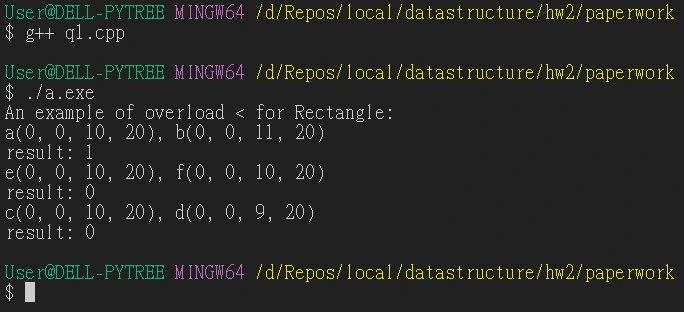
1. Overload operator< for class Rectangle.
|
|
執行結果:
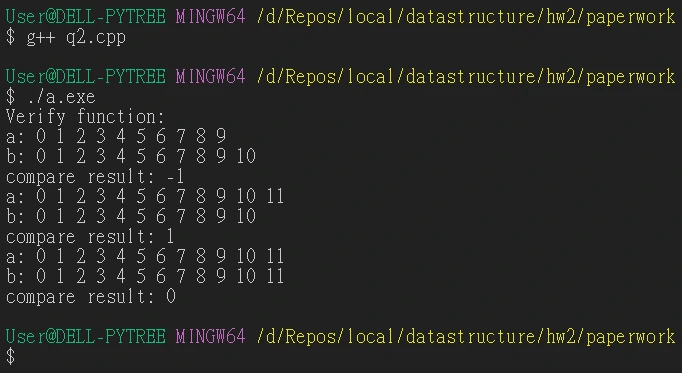
2. Write a function to compare two ordered list.
|
|
執行結果:
3. Modify function Add
- The modification is shown below, reduces the size of c.termArray to c.terms prior to termination.
- Yes, with this modification we can dispense with the data member capacity.
|
|
4. Write a C++ function that multiplies two polynomials.
假設第一個多項式 $A$ 有 $m$ 項、第二個多項式 $B$ 有 $n$ 個項,則:
- 基本運算
- 外層迴圈 $m$ 次
- 內層迴圈 $n$ 次
- 共 $mn$ 次
- 結果處理
- 每次 $m*n$ 階需尋找是否已存在相同指數的項
- 多項式最多可能有 m*n 個項
- 每次搜尋最差需要 $O(mn)$ 次比較
- 找不到相同指數的項需要
NewTerm時- 複製最多需要耗費 $O(mn)$,因為結果最多會有 $m*n$ 項
- 每次 $m*n$ 階需尋找是否已存在相同指數的項
故時間複雜度約為 $O(m^2*n^2)$
|
|
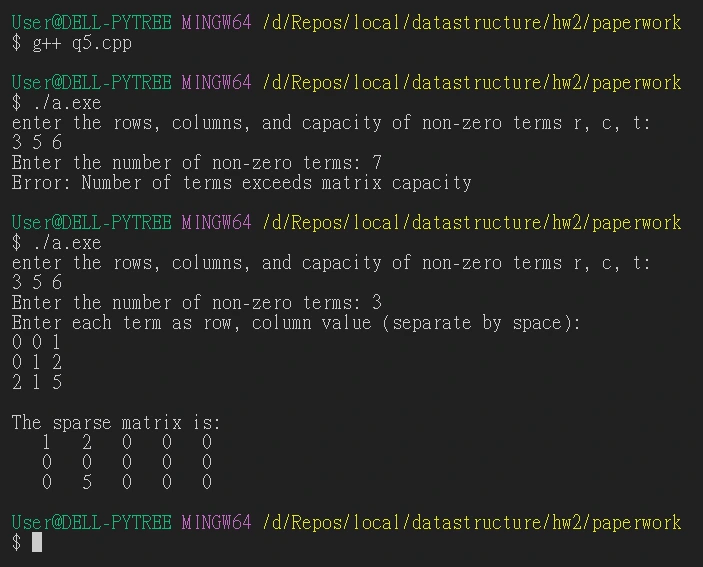
5. Write a C++ functions to input and output a sparse martrix.
operator>>的時間複雜度:$O(1)$operator<<的時間複雜度:$O(rows*cols)$
|
|
執行結果:
6. Write an algorithm that takes two strings x, y and return -1, 0, or +1.
|
|
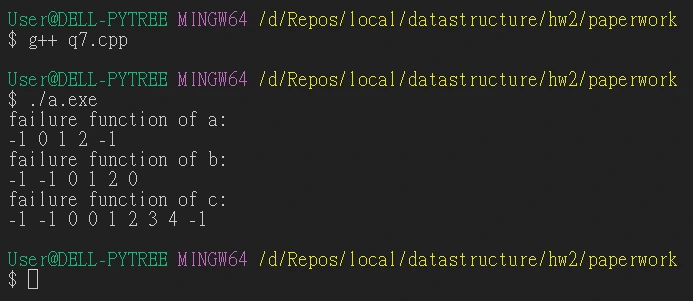
7. Compute the failure function for each of the following patterns.
|
|
執行結果:
 Junqi's Blog
Junqi's Blog